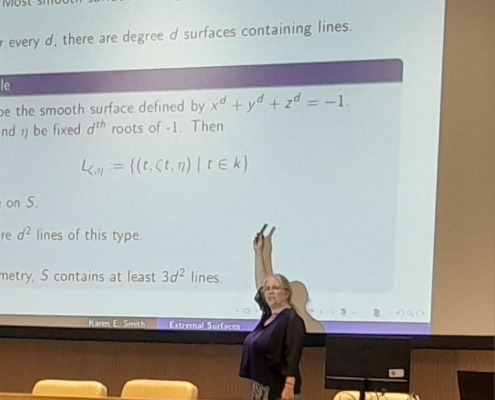Live blog 2ND AMS-UMI INTERNATIONAL JOINT MEETING - Day 4 - Sito dell'Unione Matematica Italiana

Live blog 2ND AMS-UMI INTERNATIONAL JOINT MEETING – Day 4

From July 23 to July 26, 2024, Università degli Studi di Palermo will host the 2nd International Joint Meeting co-organized by the Unione Matematica Italiana (UMI) and the American Mathematical Society (AMS). The 1st International AMS-UMI Joint Meeting was held from June 12 to June 16 2002 in Pisa.

On these pages every day we will provide live updates from the meeting: photos, short videos, events. This page will be automatically updates (if not it is enough to reload the page). Please, follow us to be updated and also on the UMI social media: Facebook, X (please, if you post some interesting content, use the hashtag #amsumi2024

To be oriented: the official website of the meeting

Complete Schedule

For more information on the campus, visit the campus map.

At this link you can see what happened yesterday!

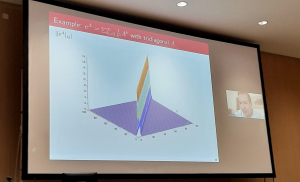
09:00 – 10:00 Invited Address Lecture, Karen E. Smith (University of Michigan)

Title: Extremal Surfaces

Abstract: Let X be a smooth complex surface in projective three-space of degree d at least 3. It is well-known that there is a quadratic upper bound on the number of lines on X in terms of d. Explicit quadratic upper bounds were given by Clebsch, Segre and others, including recently Bauer and Rams, who showed their bound works also for surfaces of prime characteristic p, provided p>d. But what about the general case of a surface whose degree might be large relative to its characteristic? In this talk, we discuss a new *sharp* upper bound on the number of lines on an arbitrary smooth surface in P³ of degree d, valid in every characteristic. This sharp bound is *quartic* in d. We also discuss some amusing properties of the “extremal” surfaces that admit these usually large numbers of lines.

10:00 – 11:00 Invited Address Lecture, Michele Benzi (Scuola Normale Superiore)

Title: An overview of localization results for functions of large matrices

Abstract : Functions of matrices (more generally, operators) have long attracted the interest of mathematicians and arise frequently in physics and other fields. An interesting property of (smooth) functions of large and sparse matrices is that they tend to be strongly localized, i.e, most of the nonnegligible entries are concentrated in certain locations; for example, if A is a banded Hermitian matrix, the entries of exp(A) decay super-exponentially in magnitude moving away from the main diagonal. This property is shared to some extent by more general matrix types and functions, with the precise rate of decay depending on the regularity of the function and on the distance between possible singularities and the spectrum (or numerical range) of the matrix. In my talk I will give an account of recent results on localization for matrix functions and describe some applications to quantum chemistry.