Risultati OCSE-PISA 2022, la prova di Matematica
Dopo l’articolo sulle prove OCSE-PISA del 12 dicembre scorso, Roberto Capone e Ketty Savioli della Commissione Italiana Insegnamento della Matematica e Francesca Ferrara del Dipartimento di Matematica dell’Università di Torino, ci offrono un ricco approfondimento sulla prova di matematica.
Con questo contributo, vogliamo approfondire alcune riflessioni a caldo che sono state pubblicate all’indomani della presentazione curata da INVALSI, a dicembre 2023, degli esiti dell’ultima indagine OCSE-PISA per studenti e studentesse quindicenni italiani.
Da allora, continua il dibattito sulla “salute” del sistema scolastico e sulle conoscenze e abilità che la scuola dell’obbligo riesce a fornire ai futuri cittadini e cittadine.
Con “salute”, possiamo intendere il complesso intreccio tra equità, qualità ed efficienza del sistema scolastico italiano, ovvero la misura in cui riesce a essere paritario e inclusivo e, contemporaneamente, presta attenzione alle necessità di un mondo in continuo e veloce cambiamento, in cui le competenze hanno un carattere più dinamico che richiede di saper discernere informazioni, di cambiare punti di vista, di risolvere problemi anche non routinari.
PISA 2022 è stata l’ottava rilevazione dal suo lancio avvenuto nel 2000.
Da allora, ogni tre anni, la prova PISA valuta le conoscenze e le abilità dei ragazzi e delle ragazze di 15 anni in matematica, scienze e lettura, concentrandosi di volta in volta su una delle tre discipline e fornendo una valutazione di sintesi delle altre due. Come sappiamo, l’ultima rilevazione (posticipata di un anno a causa della pandemia) ha focalizzato l’attenzione sulla matematica ed è stata svolta in modalità computer-based, vale a dire al computer, nella maggior parte dei Paesi partecipanti, compresa l’Italia.
Lo sguardo di PISA 2022 permette di collocare l’attuale situazione dell’Italia in relazione ad altri 80 Paesi partecipanti, di fare comparazioni e cercare analogie dunque, all’interno e all’esterno dei Paesi OCSE, ma anche di comprendere meglio i risultati locali sulla base di svariati fattori.
I risultati che ci riguardano evidenziano sia punti di forza sia disomogeneità, relative, ad esempio, a disparità legate al genere, che inducono a riflessioni importanti, non evidenti a una lettura frettolosa e assoluta dei dati.
Per poter approfondire la lettura di alcuni risultati e comprenderli appieno, però, è utile affrontare linee di discussione che fanno riferimento a questioni basilari, quali: come è strutturata una prova? Che cosa misurano gli esiti delle prove? Come si ottengono le misurazioni?
A queste domande proviamo qui a dare risposte (che non pretendiamo esaustive), fornendo informazioni che riteniamo utili anche per i non addetti ai lavori.
Come è strutturata la prova PISA di matematica?
Le prove PISA hanno come obiettivo primario quello di fornire i risultati generali a livello di popolazione piuttosto che i risultati dei singoli studenti. Per tale ragione, le scale utilizzate per la valutazione sono chiamate “scale di competenza” (proficiency) e non “scale di prestazione” (performance). Per ogni disciplina che è oggetto di valutazione, sulla base dell’andamento generale della prova, la scala di competenza descrive in modo qualitativo ciò che ragazzi e ragazze di 15 anni sanno e possono fare a determinati livelli di competenza, ma non comunica i risultati individuali che derivano dalla singola prestazione.
Vediamo come questo si configura nel caso della prova PISA di matematica.
Innanzitutto, PISA cerca di valutare non solo la capacità degli studenti di riprodurre ciò che hanno appreso, ma anche la loro capacità di applicare le conoscenze in modo creativo in scenari nuovi, di pensare in modo critico e di dimostrare strategie di apprendimento efficaci. PISA vuole valutare in tal modo la competenza (o literacy) che possiedono gli studenti quindicenni [1].
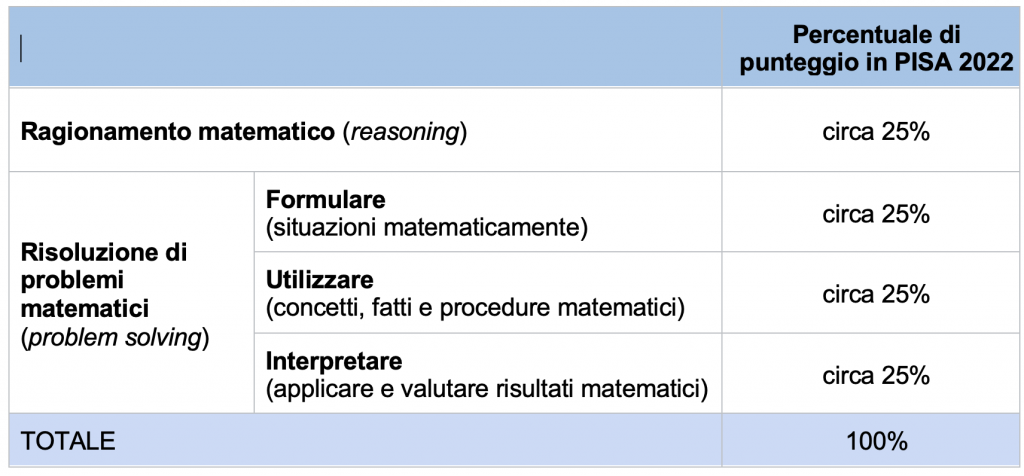
In tale ottica, gli item di matematica sono riferiti a quattro processi tipici: formulare, interpretare, utilizzare e ragionare. Mentre i primi tre processi erano già parte delle rilevazioni precedenti e pertengono alla dimensione della risoluzione di problemi in matematica, il quarto processo compare per la prima volta nel 2022 e riguarda la dimensione del ragionamento matematico.
La tabella qui sotto mostra che il “peso” attribuito ai quattro processi nella costruzione della prova è equidistribuito: la percentuale di punteggio per ciascun processo è pari a circa il 25% del punteggio totale ottenibile.
Gli item di matematica riguardano inoltre quattro ambiti di contenuto:
cambiamento e relazioni, quantità, spazio e forma, incertezza e dati, anch’essi distribuiti nella prova.
I quesiti che compongono la prova posso essere di tre tipologie:
In alcuni casi, anche in base all’articolazione della risposta aperta, PISA attribuisce un punteggio pieno (full credit) oppure un punteggio parziale (partial credit). Ciò significa che un item può anche essere valutato in modo diverso dal dicotomico 0 (errato) o 1 (corretto), come vedremo più avanti.
Come si ottiene un punteggio?
Che cosa vuol dire, ad esempio, il punteggio di 500?
L’OCSE non restituisce come risultato della prova la semplice somma dei punti attribuiti a ciascuna risposta corretta. Infatti, i risultati della prova sono punteggi riportati su una scala numerica, sopra introdotta come scala di competenza, e calcolati attraverso procedure statistiche che coinvolgono una serie di passaggi complessi.
Ma quale metodologia adotta PISA per ottenere la scala numerica?
Partiamo dalle fasi preliminari di costruzione della prova. Prima di tutto è fondamentale definire un quadro di riferimento condiviso per ogni disciplina oggetto di valutazione. Successivamente, la costruzione di nuovi item avviene aderendo rigorosamente al quadro di riferimento, mentre alcuni item di riferimento (detti item di trend) sono selezionati dalle prove precedenti (per analizzare l’andamento dei risultati nel tempo). Una terza fase consiste nella revisione qualitativa degli strumenti utilizzati per la prova da tutti i paesi partecipanti: ciò garantisce qualità e adeguatezza degli item in relazione ai vari contesti nazionali. In questa fase si sceglie la rosa finale di item che costituiranno le fasi valutative e che sono tradotti e adattati per ottenere le versioni nazionali delle prove [2].
L’attenzione si sposta quindi al processo di campionamento: PISA utilizza campioni di studenti e di item per effettuare stime sulle popolazioni.
Un campione di ragazzi e ragazze di 15 anni è selezionato per rappresentare tutti gli studenti quindicenni di un dato paese e, durante la somministrazione, ciascuno affronta una selezione di item estratti da una “banca” piuttosto ampia.
Anche se studenti diversi risolvono quesiti diversi, l’equilibrio con cui è strutturata la prova garantisce una sovrapposizione significativa di item tra le varie forme (i gruppi di item somministrati), che permette la costruzione di una scala di competenza comune a tutti gli studenti.
A questo punto, si entra nella fase cruciale in cui la scala di competenza è costruita usando modelli statistici (modelli della cosiddetta Item Response Theory) che permettono di stimare la probabile competenza di tutta la popolazione sulla base del campionamento operato.
Praticamente, la competenza mostrata nella prova da ogni studente (sotto forma di punteggio, opportunamente trasformato e tarato) è associata a una posizione specifica su una scala numerica, che indica la probabilità di rispondere in maniera corretta a ciascun item della prova [3]. Valori (o punteggi) più alti sulla scala indicano una maggiore competenza, ovvero anche una più alta probabilità di risposta corretta a ciascun item.
Sulla stessa scala sono riportati il livello di competenza dello studente (stimato) e il livello di difficoltà degli item (anch’esso stimato) [4]. Valori più alti sulla scala corrispondono così anche a item più difficili.
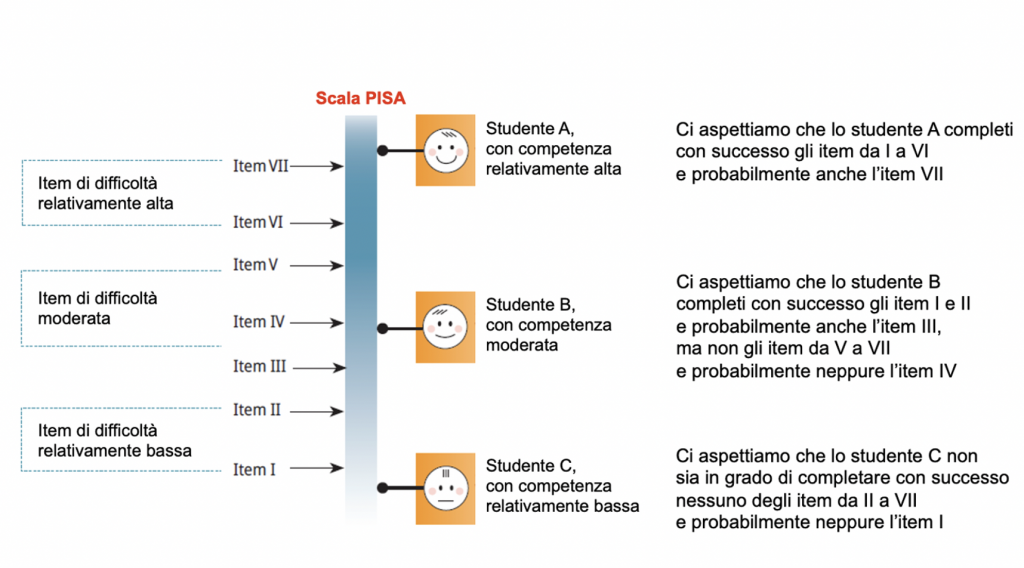
La figura seguente esemplifica una scala di competenza che va da livelli relativamente bassi di competenza (nella parte inferiore della figura) a livelli relativamente alti (verso la parte superiore). Essa mostra (a sinistra) sette item di diversa difficoltà collocati lungo la scala e (a destra) tre studenti con diversa competenza. La relazione tra la competenza degli studenti e la difficoltà degli item è descritta nella parte destra della figura.
Riassumendo, più il livello di competenza di uno studente si colloca sulla scala al di sopra della posizione di un dato item, più è probabile che lo studente possa rispondere all’item correttamente[5].
Una volta costruita la scala, è possibile descrivere il livello di competenza di ogni partecipante alla prova in base al tipo di item (ovvero al tipo di compiti) che è in grado di risolvere in modo corretto.
I risultati della prova PISA, dunque, non coincidono con la somma dei punti attribuiti alle risposte corrette o errate. I punteggi finali sono piuttosto il risultato di un complesso processo statistico che tiene conto della difficoltà degli item e di come si distribuiscono le competenze degli studenti.
I modelli statistici utilizzati da PISA descrivono così la relazione tra la competenza di ragazzi e ragazze quindicenni e le caratteristiche degli item ma non forniscono un’unità di misura per questi parametri. Perciò, PISA ha scelto un metro di misura (o una metrica) la prima volta in cui è stata stabilita una scala di competenza, vale a dire con la prima rilevazione.
In tale occasione, il punteggio di “500” sulla scala è stato definito come la competenza media degli studenti nei paesi OCSE, “100 punti di punteggio” sono stati definiti come la sua deviazione standard (una misura della sua variabilità).
All’inizio, dunque, i risultati ottenuti nella prova sono stati scalati, o “normalizzati” (cioè opportunamente trasformati e tarati) in modo che il punteggio medio nei paesi OCSE fosse approssimativamente pari a 500 punti e la deviazione standard fosse pari a 100 punti. In una tale distribuzione dei punteggi, circa due terzi degli studenti ottengono punteggi tra 400 e 600 punti.
Questo garantisce che i punteggi siano confrontabili tra i diversi paesi partecipanti e, grazie all’utilizzo della stessa scala tra valutazioni successive, anche nel tempo (con i risultati delle precedenti rilevazioni).
Per il lettore più interessato forniamo ulteriori dettagli. Mediante procedure statistiche complesse, nel tempo sono costruite prove PISA diverse ma equivalenti che hanno la stessa metrica, vale a dire che misurano la stessa cosa in modo stabile. La metrica è stabile nel tempo e indipendente dal singolo partecipante. È questo un requisito essenziale per rilevare l’evoluzione nel tempo di prestazioni di popolazioni diverse di studenti quindicenni e avere risultati comparabili.
Ciò spiega inoltre perché le prove PISA sono segretate. La prova non è rinnovata completamente ogni tre anni, è aggiornata e integrata. Per ogni rilevazione, PISA mantiene un numero significativo di item dei cicli precedenti, gli item di trend (i quali devono coprire in modo adeguato i diversi aspetti del quadro di riferimento). Sono questi che permettono di riportare sulla stessa scala i risultati di prove diverse.
Per quanto riguarda la matematica, nel 2022 erano presenti ben 74 item sviluppati e già utilizzati in rilevazioni precedenti. La loro difficoltà era perciò già stata stimata.
Le risposte fornite agli item di trend nei cicli precedenti e quelle fornite nella prova del 2022 sono state entrambe prese in considerazione durante la scalatura dei dati dell’ultima rilevazione per determinare la competenza degli studenti e la difficoltà degli item (e anche la loro capacità di discriminare tra studenti con risultati più alti e studenti con risultati più bassi). In pratica, la scala di competenza è stata calibrata nuovamente: per i nuovi item è infatti stato necessario procedere da zero al fine di stimarne i parametri, mentre per gli item di trend sono stati mantenuti i valori della rilevazione del 2018, a loro volta basati sulla calibrazione operata allora utilizzando i dati delle risposte fornite in più cicli[6].
Concludendo questa riflessione, tutte le volte in cui si opera un confronto tra punteggi è bene tenere presente che la scala è standardizzata in modo che la media sia 500 e la deviazione standard sia 100 punti. A una lettura superficiale, una differenza di 10 punti potrebbe sembrare piuttosto alta; in realtà, lo sarebbe solo se i punteggi si distribuissero in modo diverso, molto più dispersivo.
Il punteggio medio di un paese può cambiare nel tempo come risultato di miglioramenti o cali della prestazione degli studenti di livello più basso, di livello medio e di livello più alto: può cambiare cioè la differenza di prestazione tra i meno abili e i più abili, dando vita a una distribuzione dei punteggi più ampia o più ristretta, con una media diversa.
Secondo i risultati dell’indagine PISA 2022, i punteggi medi dei paesi OCSE sono stati pari a 472 in matematica, 476 in lettura e 485 in scienze.
In matematica, gli studenti italiani hanno ottenuto un punteggio medio (471 punti) che differisce di un solo punto dalla media OCSE. Per i risultati in lettura va ancora meglio, dal momento che l’Italia mostra una prestazione media (482 punti) più alta del punteggio medio dei paesi OCSE. Per le scienze, infine, l’Italia ha ottenuto un punteggio medio pari a 477 punti, 8 punti sotto la media OCSE.
Rispetto alla rilevazione del 2018, la prestazione media dei paesi OCSE in PISA 2022 è diminuita di ben 15 punti in matematica e di 10 punti in lettura. Nessuna differenza significativa invece per le scienze, per cui il punteggio medio è rimasto relativamente stabile nel 2022 pur se leggermente diminuito (di 2 soli punti). In Italia, la prestazione media in matematica nel 2022 ha subito lo stesso calo di 15 punti da quella del 2018, mentre le prestazioni in lettura e in scienze sono entrambe migliorate (di 5 e 9 punti; solo la seconda differenza risulta statisticamente significativa).
Quali sono i livelli di competenza in matematica?
Nella rilevazione del 2012, la penultima volta in cui la matematica è stata l’ambito principale della valutazione, la scala di competenza era suddivisa in sei livelli, da 1 a 6. Con l’ultima rilevazione, il livello 1 per la matematica è stato ulteriormente suddiviso nei livelli 1a, 1b e 1c, allo scopo di descrivere meglio che cosa sanno fare gli studenti che si collocano all’estremità inferiore della scala di competenza. Il nuovo livello 1a corrisponde al precedente livello 1.
A tal proposito, evidenziamo che quesiti più facili hanno nel tempo arricchito la prova proprio per poter rilevare e descrivere il tipo di literacy matematica che caratterizza i livelli più bassi. Anche per questa ragione, il termine literacy utilizzato dal PISA non va erroneamente inteso (tradotto) come alfabetizzazione: essere a un livello relativamente basso non significa essere analfabeta, piuttosto significa essere “in grado di fare solo certe cose”.
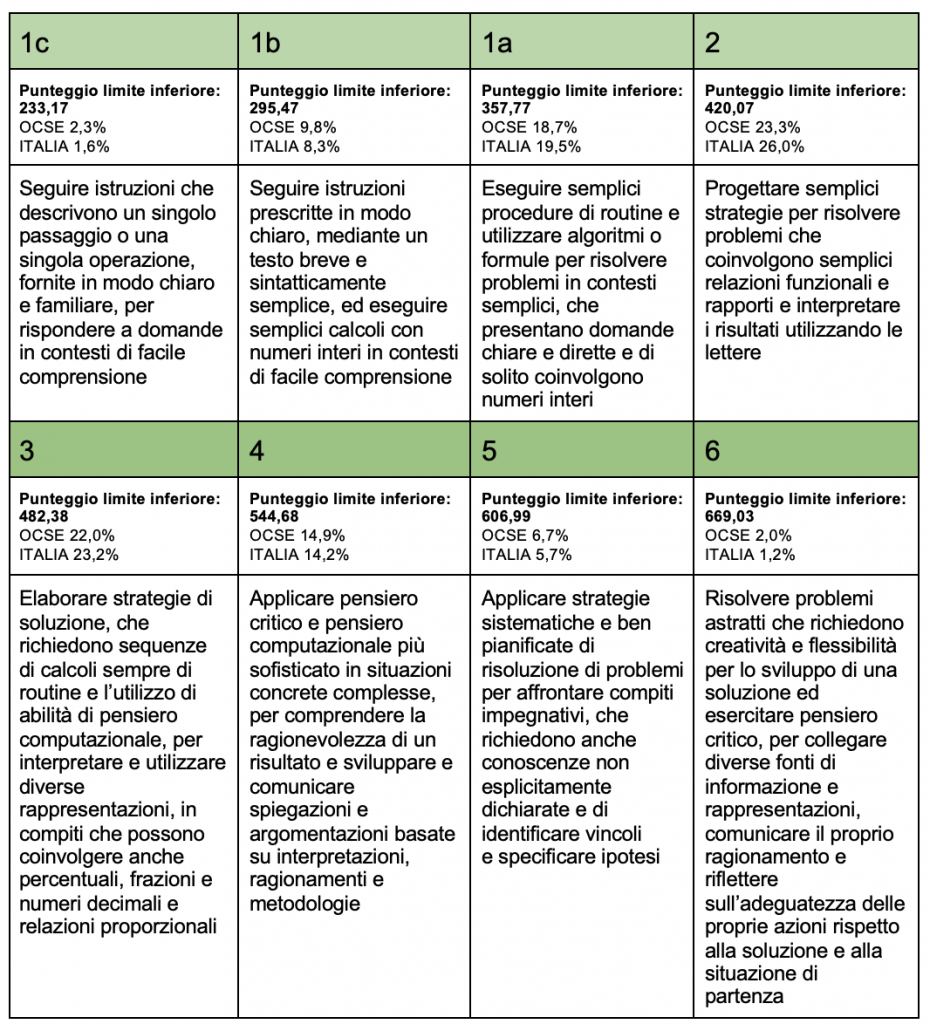
La scala di competenza per la matematica costruita dalla prova PISA del 2022 è così costituita da otto livelli. La tabella sotto sintetizza la descrizione degli otto livelli di competenza e mostra che ogni livello copre un intervallo di circa 62 punti. Possiamo pertanto considerare differenze di punteggio di tale entità come la differenza in termini delle conoscenze e abilità che sono descritte da livelli di competenza successivi. Le percentuali mostrate si riferiscono invece alla percentuale di studenti che si colloca almeno a quel livello (ad es., solo il 26% di quindicenni italiani si colloca almeno a livello 2 e solo il 14,2% almeno a livello 4).
È bene ricordare che queste descrizioni per i livelli di competenza sono create solo a posteriori, in base ai risultati della prova. Dunque, sono descrizioni contingenti e non assolute, legate alle conoscenze e abilità matematiche specifiche messe in campo dagli item che costituiscono la prova.
Il rapporto di PISA 2022 introduce nella discussione dei risultati anche la distinzione tra coloro che ottengono un punteggio sotto il livello 2 e coloro che raggiungono il livello 5 o superiore (i cosiddetti low performer e top performer, rispettivamente).
Chi sono i low-performer e i top-performer?
Per tutte le discipline, il livello 2 è considerato il livello minimo di competenza che tutti gli studenti quindicenni dovrebbero avere. Gli studenti di livello 2 possiedono un livello base di competenza: in termini pratici, sono in grado di utilizzare algoritmi di base e semplice conoscenza scientifica e di interpretare semplici testi. Gli studenti che si collocano a livello 1a, 1b o 1c hanno una competenza più fragile, mentre coloro che si collocano a livello 3 o 4 sono studenti con competenza moderata. Gli studenti che raggiungono il livello 5 o il livello 6 hanno invece competenza alta: sono in grado, ad esempio, di lavorare in modo efficace con modelli matematici per situazioni complesse, di interpretare e valutare esperimenti complessi e di comprendere testi astratti.
I risultati di PISA 2022 mostrano un dato importante in relazione alla matematica: in media, nei paesi OCSE, il 31,1% di ragazzi e ragazze di 15 anni ancora si trova sotto il livello 2 di competenza matematica. Nel caso dell’Italia, la percentuale si attesta vicino alla media OCSE: il 29,6% non raggiunge il livello 2. Solo il 6,9% degli studenti italiani si colloca invece a un livello 5 o 6 (contro l’8,7% della media OCSE).
La distinzione tra low e top performers è importante, perché le informazioni che la rilevazione fornisce su questi gruppi di studenti possono essere utilizzate per meglio comprendere anche eventuali disuguaglianze, come quelle legate al genere, che approfondiremo in un successivo contributo.
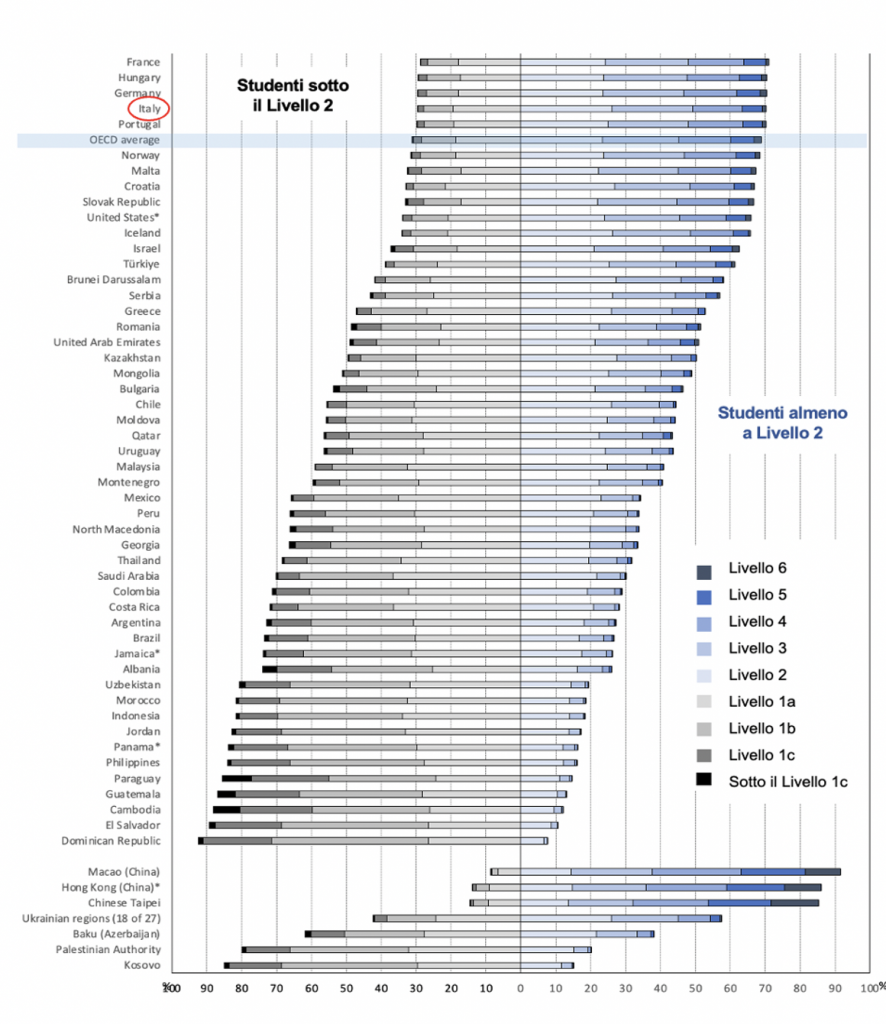
Il seguente grafico mostra, in quarta posizione dall’alto, le percentuali di studenti italiani ai diversi livelli (per praticità, il grafico è stato tagliato nella parte superiore, escludendo i 23 paesi che hanno ottenuto i risultati migliori come, ad esempio, i paesi dell’est asiatico, la Finlandia, il Canada, l’Estonia). La media OCSE è visibile due posizioni più in basso dell’Italia.
Quale può essere una richiesta fatta all’interno della prova?
La prova PISA 2022 è costituita da richieste che sono spesso raggruppate in unità. Il termine unità, in gergo tecnico, è utilizzato per indicare un contesto comune al quale si riferiscono più item.
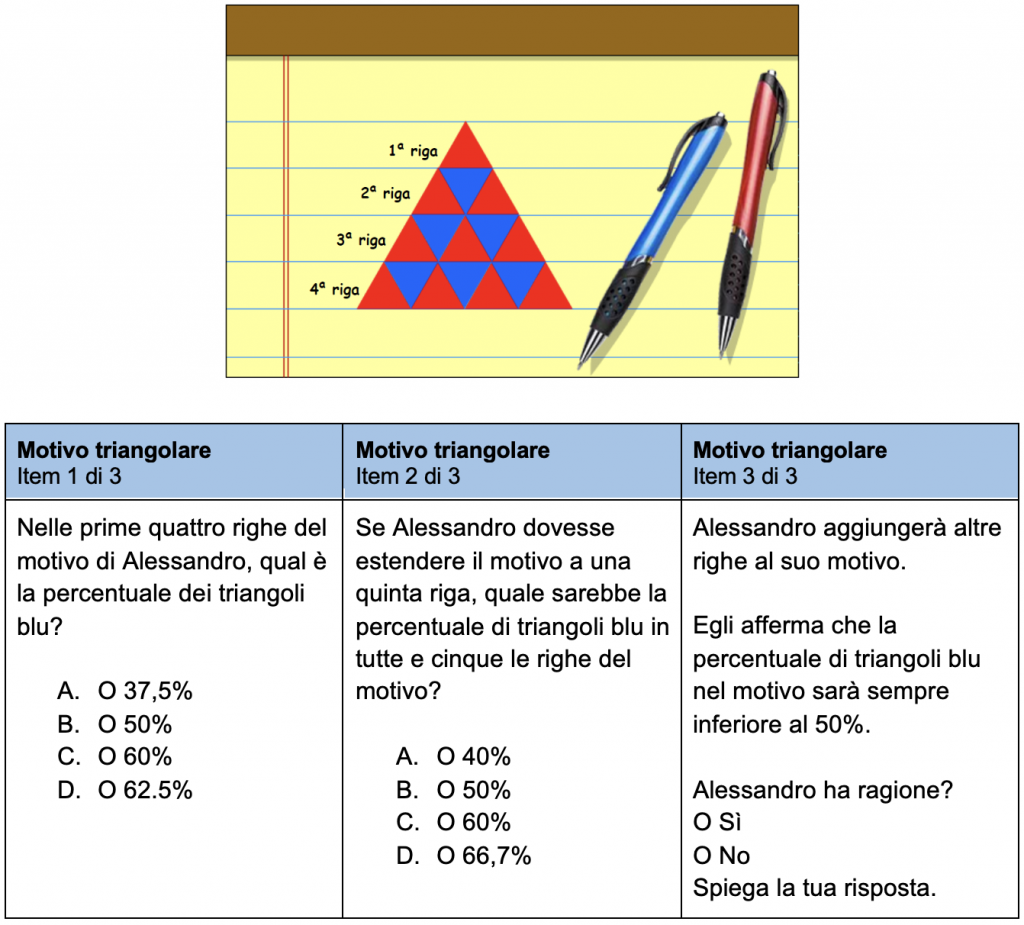
Analizziamo un esempio di unità rilasciato per capire la sua indicizzazione e le informazioni che ci fornisce rispetto al tipo di abilità e di pensiero critico valutati nella prova. L’unità Motivo triangolare è composta da tre item focalizzati su richieste che spingono verso competenze diversificate, partendo dallo stesso stimolo visivo di un pattern, vale a dire una regolarità espressa mediante uno schema, un motivo, una sequenza.
Consideriamo i tre item che si agganciano a questo stimolo [7] .
MOTIVO TRIANGOLARE
Alessandro ha disegnato il seguente motivo a triangoli rossi e blu.
Le prime quattro righe del motivo sono illustrate qui sotto.
ITEM 1 di 3
L’item è così indicizzato: l’ambito di contenuto è quantità e il processo è utilizzare concetti, fatti e procedure matematici. Si tratta di un item a scelta multipla.
Le prime quattro righe del motivo sono visibili e si può procedere direttamente. Attraverso un conteggio, si individua che i triangoli blu sono 6 su 16 triangoli in tutto. Calcolando la percentuale, con l’algoritmo classico, si ottiene 37,5% (tra l’altro, gli studenti hanno a disposizione una calcolatrice all’interno dell’applicativo).
Si può anche ragionare per esclusione: i triangoli blu sono meno della metà di 16.
Dunque l’unica opzione che corrisponde a una percentuale minore del 50% è 37,5%.
L’opzione B, cioè 50%, rivela un errore di conteggio evidente.
Invece l’opzione C si basa sul rapporto “blu su rossi” anziché sul rapporto “blu su tutti i triangoli” per concludere che i triangoli blu sono 6 su 10 cioè il 60% di tutti i triangoli.
L’opzione D, analogamente, intercetta l’utilizzo del rapporto “rossi” anziché blu “su tutti i triangoli” e dunque il calcolo 10 su 16 cioè 62,5%.
Al di là della percentuale di risposte corrette ottenuta a livello internazionale, che non ancora stata rilasciata, l’item si presta a riflessioni di tipo didattico, dal momento che i distrattori catturano errori di calcolo o l’eventuale applicazione di formule o procedure tralasciando sistemi di controllo o di ragionamento, che potrebbero invece agevolmente portare alla risposta corretta o all’esclusione delle altre opzioni di risposta.
Dal punto di vista della sua difficoltà, l’item si aggancia a un livello 1a come definito nella tabella sopra: coinvolge infatti un contesto semplice con una domanda posta in modo chiaro e diretto, che richiede l’utilizzo di numeri interi e di semplici procedure di routine.
ITEM 2 di 3
L’ambito di contenuto del secondo item è relativo a cambiamento e relazioni mentre il processo è formulare.
La richiesta varia rispetto all’item 1 poiché chiede di immaginare che cosa succede alla percentuale di triangoli se si inserisce anche la quinta riga, che non è disegnata. L’impostazione e le strategie di risoluzione sono analoghe a quelle della richiesta precedente, anche il formato rimane quello della scelta multipla.
In questo caso, la soluzione si basa sul rapporto tra 10 triangoli blu e 25 triangoli in tutto nelle 5 righe, che equivale a una percentuale del 40%.
L’opzione B, cioè 50%, rivela un errore di conteggio evidente: considera infatti il numero di triangoli rossi uguale al numero di triangoli blu.
L’opzione C tiene conto del rapporto tra i triangoli rossi e tutti i triangoli (15 su 25 cioè 60%). L’opzione D, infine, tiene conto del rapporto tra triangoli blu e triangoli rossi (10 su 15 cioè 66,7% approssimato).
Per trovare la soluzione corretta si può procedere in diversi modi.
Aggiungendo la quinta riga immaginaria e individuando che i triangoli blu sono 10 su 25, con l’algoritmo classico, si ottiene 40%. Oppure si può usare un ragionamento proporzionale: 10 su 25 equivale a 40 su 100 dunque il 40%.
Un’altra strategia, più rapida, vantaggiosa rispetto alla variabile tempo, coinvolge capacità di visualizzazione e la connessione di informazioni con cui evincere che, per ciascuna riga, il numero dei triangoli blu è sempre minore del numero dei triangoli rossi: ciò permette di concludere che complessivamente i triangoli blu sono meno del 50% e di escludere tutte le altre opzioni mantenendo solo la risposta A.
Questo secondo item si aggancia a un livello 2 di competenza: richiede infatti di utilizzare semplici strategie che coinvolgono rapporti in un contesto nel quale le informazioni da utilizzare non sono tutte esplicite.
ITEM 3 di 3
L’ultimo item relativo al motivo triangolare coinvolge ancora cambiamento e relazioni come ambito di contenuto e lavora sulla generalizzazione, sulla base della relazione tra triangoli rossi e triangoli blu con cui è costruito il motivo. Si tratta di un item a risposta aperta, strutturato per misurare competenze più argomentative che richiedono anche di fornire una spiegazione del “perché” matematico. ll processo è infatti in questo caso ragionare.
L’item prevede una correzione con punteggio pieno (in tal caso si colloca al livello di competenza 5) oppure con punteggio parziale (in tal caso si colloca al livello di competenza 4). Si tratta di un item di difficoltà alta.
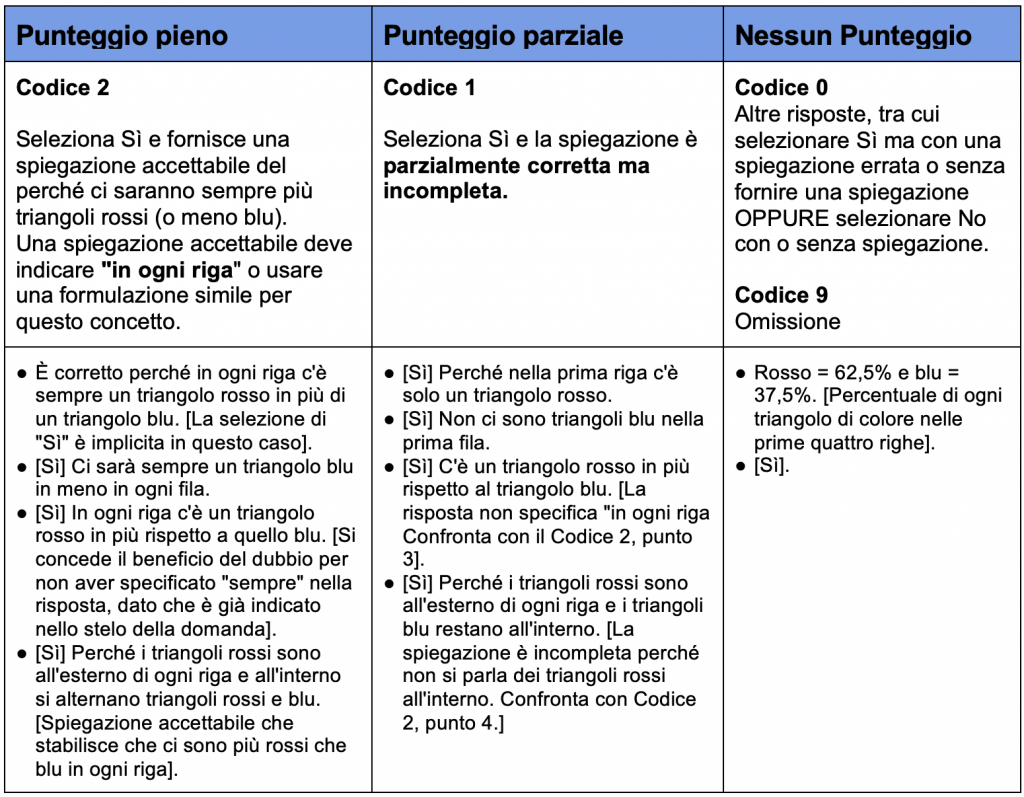
In questo caso merita fare un approfondimento sulla griglia di correzione (riportata sotto), necessaria per definire i confini di accettabilità delle spiegazioni fornite dagli studenti e la conseguente attribuzione di un punteggio pieno o parziale. La griglia non è esaustiva ma fornisce dei riferimenti, comunque rappresentativi del tipico modo di rispondere degli studenti, per valutare la completezza o meno di una spiegazione, fermo restando che si tratta di un tipo di item che richiede una codifica da parte di esperti.
Possiamo osservare che, per ottenere un punteggio almeno parziale, è necessario in qualche modo esplicitare una relazione tra il numero di triangoli rossi e il numero di triangoli blu: ad es. “un triangolo rosso in più rispetto al triangolo blu” (livello di competenza 4). Per ottenere un credito totale, è necessario in aggiunta che la relazione sia riferita a ogni riga del motivo, esplicitando il vincolo che permette la generalizzazione (livello di competenza 5).
L’esempio di questo item, che riguarda la dimensione del ragionamento matematico, ci aiuta a riflettere sull’importanza dei processi argomentativi nella didattica della matematica. Si tratta di processi complessi, come anche esprime la variabilità delle spiegazioni nella griglia; di processi profondi, essenziali per sviluppare strumenti di controllo per la gestione di compiti pur impegnativi e per stimolare la capacità di spiegare opportunamente le risposte fornite.
Il rapporto PISA 2022, oltre al risultato medio in matematica, restituisce un punteggio medio specifico per ciascuno dei quattro processi. Per quanto concerne ragionare, ragazzi e ragazze italiani hanno ottenuto 474 punti, un risultato in linea con la media OCSE (474) e più alto dei punteggi relativi a formulare, utilizzare e interpretare (464, 470 e 471, rispettivamente).
Indipendentemente dal livello di competenza, si tratta di un risultato positivo: infatti, il ragionamento non richiede necessariamente una matematica avanzata ma una netta comprensione di concetti fondamentali e coinvolge il pensare in modo indipendente. Per tale ragione, spiegazioni e argomentazioni matematiche dovrebbero diventare la norma nelle pratiche d’aula quotidiane, dove è fondamentale che ragazzi e ragazze sappiano ragionare in matematica, così da esercitare pensiero critico e creatività, due tra le cruciali abilità richieste per i cittadini del XXI secolo.
In un prossimo approfondimento, tratteremo più specificatamente gli ultimi dati PISA in relazione al tema delle disuguaglianze, con particolare attenzione agli esiti relativi alla disparità di genere. Si tratta di una problematica urgente, verso gli obiettivi di sviluppo sostenibile dell’Agenda 2030 delle Nazioni Unite riguardanti un’educazione equa e paritaria.
[1] Il costrutto di literacy matematica è definito come la capacità di ragionare matematicamente e formulare, utilizzare e interpretare la matematica per risolvere problemi in una varietà di contesti della realtà. Include concetti, fatti, procedure e strumenti per descrivere, spiegare e prevedere fenomeni. Aiuta le persone a fornire giudizi fondati, a prendere decisioni e a diventare cittadini del XXI secolo riflessivi, impegnati e costruttivi.
[2] Si tratta di una fase piuttosto lunga che comprende anche una prova sul campo (il cosiddetto field trial): la rosa di item selezionati e tradotti per le versioni nazionali è presentata a un campione di ragazzi e ragazze quindicenni in tutti i paesi partecipanti. Il field trial ha lo scopo di assicurare gli standard qualitativi e la comparabilità dei risultati della prova a livello internazionale: in particolare, permette di verificare, a livello psicometrico, l’equivalenza degli item tra paesi diversi. Una volta avvenuta la prova sul campo, gli item utilizzati sono scartati, revisionati o mantenuti per costituire l’insieme finale di item potenziali, da cui si scelgono gli item per le prove nazionali (che sono nuovamente soggetti a revisione da parte di tutti i paesi).
[3] Questo processo avviene infatti tenendo conto di tutte le risposte che lo studente ha dato a tutti gli item contenuti nella sua prova.
[4] Anche la difficoltà di ciascun item è ottenuta tenendo conto di tutte le risposte fornite a quello specifico item.
[5] L’attribuzione di un certo livello a uno studente non esclude la possibilità che lo studente possa rispondere in maniera corretta anche a item di livello di difficoltà più alto.
[6] La difficoltà relativa di alcuni item di trend o la loro capacità di discriminare può cambiare nel tempo. Se ciò accade tra due rilevazioni successive, si ha un “errore di collegamento” (o link error, espresso in tot punti di punteggio) che quantifica il grado di incertezza coinvolto in confronti dei risultati nel tempo. PISA incorpora l’incertezza associata a tali cambiamenti quando calcola la significatività statistica delle stime degli andamenti nel tempo.
[7] La versione che qui utilizziamo è quella originale della prova di matematica somministrata in Italia.
(a cura di Roberto Capone e Ketty Savioli, Commissione Italiana Insegnamento della Matematica; Francesca Ferrara, Dipartimento di Matematica – Università di Torino)
Per approfondimenti:
Sito internazionale OCSE: https://www.oecd.org/pisa/
INVALSI – Area prove internazionali – PISA 2022:
https://invalsi-areaprove.cineca.it/index.php?get=static&pag=ocse_pisa_info
Primo contributo UMI CIIM dicembre 2023: Qualche commento sui risultati dell’indagine PISA 2022
Qui il testo completo in pdf.